Dabbling in Computational Linguistics

18 Sep 2014

• unramblings
• linguistics

About a month ago, /u/5outh posted an article called Modeling and Simulating Markov Chain Evolution in Haskell to /r/haskell. It’s an interesting read, and it has a fairly amusing conclusion — a twitter account called rapcandy that gives a single line of stochastic rap every day, using patterns drawn from the wisdom of Eminem.

For a given sequence of things (be they words in a sentence, letters in a word, musical notes in a melody, etc.), we have that for every given pair of things, say a and b, there is a certain probability of b following a in the sequence, which we call the transition probability. So for example in the sequence:

\[ 1, 2, 3, 1, 3, 3, 2, \text{end} \]

The transition probabilites are:

\[ \begin{array}{rclcl} 1 & \mapsto & 1 & : & 0 \\ 1 & \mapsto & 2 & : & 1/2 \\ 1 & \mapsto & 3 & : & 1/2 \\ 1 & \mapsto & \text{end} & : & 0 \\ 2 & \mapsto & 1 & : & 0 \\ 2 & \mapsto & 2 & : & 0 \\ 2 & \mapsto & 3 & : & 1/2 \\ 2 & \mapsto & \text{end} & : & 1/2 \\ 3 & \mapsto & 1 & : & 1/3 \\ 3 & \mapsto & 2 & : & 1/3 \\ 3 & \mapsto & 3 & : & 1/3 \\ 3 & \mapsto & \text{end} & : & 0 \\ \end{array} \]

These probabilities represent data from which we can now generate new sequences which are like the original sequence. For example, we might decide to start with 1. Then we see that 1 can be followed by either 2 or 3, each with probability 1/2, so we flip a coin and choose 2 for heads and 3 for tails, and assign it to be the next number in the new sequence. If we got a 3, we would do the same as before: 3 can be followed by 1, 2, or 3, each with equal probability, so we flip a three sided coin¹ and assign the next number accordingly. Eventually we will² end up with a sequence that is like the old one.

As said above, this method can work with more than just numbers. rapcandy uses it on sequences of words in rap to generate new rap like phrases.

Verbogenesis

I wanted to see how well I could apply the method to words. Instead of sequences of numbers, words are sequences of letters, but the exact same logic as above applies readily. It wasn’t too hard to whip up a script to calculate the transition probabilities from a list of words, and also to generate new words from the probabilities.

The first thing I thought to test it on was a list of names. Given the names Hannah, Sophie, Josh, and Charlotte, it began to spit back things like “Sophannah”, “Chie”, and “Josophie”.

I happened to have a list of around 50,000 English words on my laptop, used for spell checking. I gave the list to the program to chew on, and after about 15 minutes I started getting back things like the following:

xcckpontommat
ficadinsy
kisiode
huesig
hrarimui
condinte
hidoblylesch
bjung
umunghricetit
verang
anthic
uoatitesined
upinis
blchiongr
coore
pusigmers
gethilur
ogrowhil
hinbs
zasounterims
...

This is promising. Things like “anthic” or “coore” seem fairly legitimate as words go. Unfortunately others like “xcckpontommat” aren’t quite so satisfactory. What’s going wrong? The answer lies in noticing that sounds and letters in the English language do not have a one to one mapping. For example, two letter sounds such as “th” are not going to be adequately represented in the probabilities calculated above.

I decided to modify the algorithm to use transition probabilities not from a single letter to a single letter, but from two sequential letters to the following single letter³. Unfortunately now the calculations necessary to produce the transition probabilities were taking too long, so once I got home I rewrote the script in a heavily optimised fashion and ran it on my more powerful desktop computer. With the new code I was able to calculate the probabilities in less than a minute, and generate words like the following:

sincesspriter
excastboarm
panations
pikindpitasteter
unteraikinitutdons
bowborehonemenes
suaftys
nock
kadooteltzs
res
foldennomsencoadisolanions
ned
poots
uning
mist
undamellons
headampucks
forgisirestors
mirbles
otte
...

Much better than before! Almost all of these sound and look like they could be real English words.

Multilingual Verbogenesis

I wanted to make sure that these words really did sound English, and that it wasn’t simply that they were pronounceable. Was it possible that if I used dictionaries in other languages, the generated words would look representative of those languages? The hypothesis seemed likely but I wanted to verify it, so I downloaded dictionaries for 24 different languages and generated some words from each. I think the results speak for themselves. Here are some examples:

French

maduchemplas
delumevaluttreat
tasseraisomploirai
nemimbrez
dentapretament

German

spendestrattet
eittufdrabstettschtiside
vereitzusgem
kars
uben

Italian

colo
dabbrabbarielle
bravvancibuonimbramocele
ciamo
alatiscelli

Polish

forpisurdepaliy
zartyz
niabysies
niezgarciby
akazkaysmysobaste

All this is very good, but doesn’t really seem to serve any real purpose (apart from confusing learners of languages). Is there any way we can use the data we now have to produce anything meaningful?

Language Distance

If you’re still reading this article, chances are you know about Pythagoras’ theorem. The length on a graph from the point $(x_1,y_1)$ to the point $(x_2,y_2)$ is equal to $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$. This generalises to more than two dimensions. The length on a graph from the point $(x_1,y_1,\dots)$ to the point $(x_2,y_2,\dots)$ is equal to $\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + \dots}$.

We call the set of transition probabilities for a given language its transition matrix. Suppose we have a many dimensioned graph, whose axes represent transition probabilities. Then each language’s transition matrix is a point on this graph, and fundamentally we can calculate distances between these points using the exact formula given by Pythagoras’ theorem above. We’ll call this distance the language distance.

I calculated the language distances for all the pairings of the processed languages; a subset is shown below:

	British English	Catalan	Finnish	French
British English	0	15.03	16.20	14.36
Catalan	15.03	0	16.94	15.96
Finnish	16.20	16.94	0	16.91
French	14.36	15.96	16.91	0

These numbers aren’t very easy to look at and spot patterns in.

Dendrogrammar

This problem relates to one in phylogenetics. When faced with a set of genetic data for different species, geneticists commonly wish to figure out which species are most related, and to depict such relations graphically. A solution is to use Hierarchical Clustering to plot a graphic known as a dendrogram, an example of which is given below.

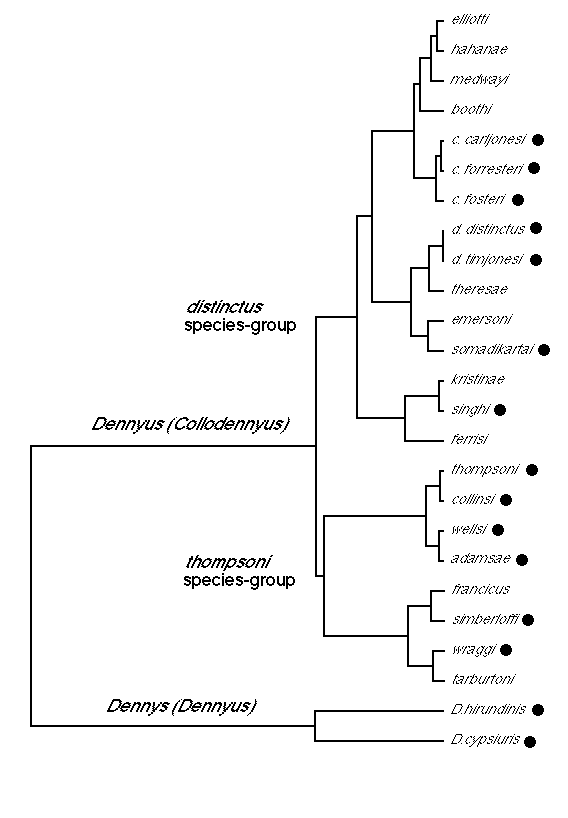
This graph is from the Zoology department at the University of Glasgow (more info here). It can be viewed rather like a family tree.

I thought this seemed like a great solution to the undecipherable table of numbers shown above, so I decided to generate a dendrogram for the languages I processed. The result is below.

This is much easier to understand than the table, and even seems to show mostly reasonable results. For example, the three Englishes are all grouped tightly together (with US and Canadian English matching closest), as are the two Frenches, and Catalan and Valencian. There seem to be main groupings in the diagram vaguely aligning with geography.

One curve ball is Indonesian being linked with croatian and finnish, but we have to remember that this diagram is based on written language, specifically the Latin alphabet. Indonesian didn’t have a writing system until the turn of the 20th century (created in fact by Dutch colonists), so this method may not give very meaningful results about Indonesian.

Do it yourself

I find it remarkable that such an informative diagram can be produced in such a relatively simple way, and it is a fantastic feeling to be able to generate such a thing from the raw dictionaries of words.

The code that I used is open source and available here. Feel free to use it however you like.

---

---